Tangent and Normal of a Circle
Tangent and Normal of a Circle: Overview
This topic covers concepts, such as, Tangent to a Circle, Equation of Tangent to a Circle, Director Circle of a Circle & Normal to a Circle etc.
Important Questions on Tangent and Normal of a Circle
The equation of circle such that the length of the tangent to it from the points and are respectively, is
Let ABCD be a quadrilateral with area 18, with sides AB parallel to the side CD and AB = 2CD. Let AD be perpendicular to AB and CD. If a circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is
Consider a circle S with centre at the origin and radius . Four circles and each with radius unity and centres and respectively are drawn. chord of the circle touches the circle and passes through the centre of the circle . If the length of this chord can be expresses as , find .
The lines and are tangents to the same circle. The radius of this circle is
The area of the triangle formed by the positive -axis, the normal and the tangent to the circle .
Consider the circle that passes through the points and having the smallest area. Then, the equation of the tangent to the circle at is
Find the slope of the focal chords of the parabola , which are tangents to the circle
If the lines are tangents to a circle, then find the radius of the circle.
Find the parametric coordinates of the circle and also, find the equation of the tangent using the parametric coordinates.
The equation of normal which is at a maximum distance from and drawn to the circle is
The tangent at on the circle touches the circle at . Then, a point of trisection of is
The length of the diameter of circle whose normal at the point cuts the circle again at point common to the line and is
The tangent to the circle at the point cuts off a chord of length from a circle whose centre is The radius of is :-
Centres of two circles having radius and units respectively are units apart. The area of the quadrilateral formed by joining the points of contact of external tangents drawn to two circles is equal to (in sq. units)
The tangent to the circle at the point cuts off a chord of length from a circle whose centre is . The radius of is
For next two question please follow the same
A tangent line is drawn to a circle with unit radius at the point and a segment is laid off whose length is equal to that of the arc , a straight line is drawn to intersect the extension of the diameter at the point .
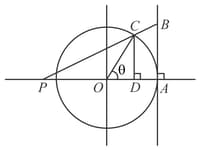
The area of the trapezoid is
Let be the circle concentric with the circle, and having area of the area of this circle. Then a tangent to parallel to the line, makes an intercept on the -axis, which is equal to
From a fixed point on the circumference of a circle of radius , is the perpendicular on the tangent at of the circle, then maximum area of the triangle is equal to
The smaller of the circle touching the straight lines at and the line , has radius , then =
Let consider a point outside the circle with centre at , tangents and are drawn such that
, then length of chord is
