Basics of Parabola

Find the auxiliary circle for parabola $x^2+4x+4y+16=0$.

The vertex of a parabola is $\left(1,2\right)$ and its axis is parallel to $y-\mathrm{axis}$. If parabola passes through $\left(0,6\right)$, then the length of its latus rectum is _____

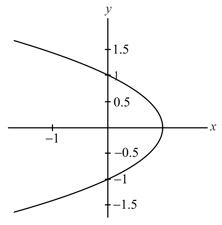
The function corresponding to the graph shown below is

The vertex of the parabola $x^2=8y-1$ is

If $x-2=t^2,y=2t$ are the parametric equations of the parabola $y^2=a(x-b),$ then the value of $a+b$ equals

If the line $2bx+3cy+4d=0$ passes through the points of intersection of $y^2=4ax$ and $x^2=4ay,$ then $\_\_\_\_\_\_\_$

The parametric equation of a parabola is given by $x=1-2t, y=2t^2-2$. The length of latus-rectum of the parabola is

The co-ordinates of one of the end points of the latus-rectum of the parabola $(y-1{)}^2=2\left(x+2\right)$ are

If the co-ordinates of one end-point of a focal chord of the parabola $y^2=32x$ are $\left(2, -8\right)$, then the co-ordinates of other end-point are

If the equation of the directrix of the parabola $y^2-kx+8=0$ is $x-1=0$, then $k=$

If the straight line $2x-y=8$ is a focal chord of the parabola $y^2=ax$ then the equation of the directrix is

If the straight line $2x+y+\lambda =0$ is a focal chord of the parabola $y^2=-8x$, the value of $\lambda$ is

The length of latus-rectum of the parabola $169\left[(x-1{)}^2+(y-3{)}^2\right]={\left(5x-12y+17\right)}^2$ is

The co-ordinates of the point of intersection of the axis and the directrix of the parabola $x^2+4x+4y+16=0$ are

If the co-ordinates of the vertex and focus of a parabola are $\left(1, 4\right)$ and $\left(2, 6\right)$ respectively, then the equation of its directrix is

If the co-ordinates of the vertex and the focus of a parabola are $\left(-1, 1\right)$ and $\left(2, 3\right)$ respectively, then the equation of the directrix is

If the parametric equation of a parabola is $x=t^2+1, y=2t+1$, then the Cartesian equation of the directrix is

The equation of the directrix of the parabola $y^2+4x+3=0$ is

For a parameter $t$ the locus of the point $\left(2t-3, 4t^2-1\right)$ is

If $t$ be a parameter then the locus of the point $P\left(2a {\cos }^2 t, 2a \cos t\right)$ represents