Equation of Continuity

A laminar stream is flowing vertically down from a tap of cross-section area 1 cm². At a distance 10 below the tap, the cross-section area of the stream has reduced to 1/2 cm^​2. Find the volumetric flow rate of water from the tap

A cylindrical vessel open at the top is 20 cm high and 10 cm in diameter. A circular hole whose cross-sectional area 1cm² is cut at the centre of the bottom of the vessel. Water flows from a tube above it into the vessel at the rate 100 cm³ s^​-1 . Find the height of water in the vessel under steady state.

Water from a tap emerges vertically downwards with an initial speed of $1.0\mathrm{ }\mathrm{m}{\mathrm{s}}^{-1}$ . The cross $-$ sectional area of the tap is ${\mathrm{ }10}^{-4}\mathrm{ }{\mathrm{m}}^2$ . Assume that the pressure is constant throughout the stream of water and that the flow is streamlined. The cross $-$ sectional area of the stream, $0.15\mathrm{ }\mathrm{m}$ below the tap would be:
(Take $\mathrm{g}=10\mathrm{ }\mathrm{m}{\mathrm{s}}^{-2}$ )

An ideal fluid flows (laminar flow) through a pipe of non-uniform diameter. The maximum and minimum din meters of the pipes are $6.4 \mathrm{c}\mathrm{m}$ and $4.8 \mathrm{c}\mathrm{m}$ , respectively. The ratio of the minimum and the maximum velocities of fluid in this pipe is:

Water from a tap emerges vertically downwards with an initial speed of $1.0\mathrm{ }\mathrm{m} {\mathrm{s}}^{-1}$. The cross -sectional area of the tap is ${\mathrm{ }10}^{-4}\mathrm{ }{\mathrm{m}}^2$ . Assume that the pressure is constant throughout the stream of water and that the flow is streamlined. The cross-sectional area of the stream, $0.15\mathrm{ }\mathrm{m}$ below the tap, would be:
(Take $g=10\mathrm{ }\mathrm{m} {\mathrm{s}}^{-2}$ )

Water is moving with a speed of $5.18 \mathrm{m} {\mathrm{s}}^{-1}$ through a pipe with a cross-sectional area of $4.20 {\mathrm{cm}}^2$. The water gradually descends $9.66 \mathrm{m}$ as the pipe increases in area to $7.60 {\mathrm{cm}}^2$. The speed of flow at the lower level is

Water is flowing at a speed of $1.5 \mathrm{m} {\mathrm{s}}^{-1}$ through a horizontal tube of cross-sectional area ${10}^{-2} {\mathrm{m}}^2$ and you are trying to stop the flow by your palm. Assuming that the water stops immediately after hitting the palm, the minimum force that you must exert should be (density of water $={10}^3 \mathrm{kg} {\mathrm{m}}^{-3}$)

If the velocity head of a stream of water is equal to $10 \mathrm{cm}$, then its speed of flow is approximately ( in $\mathrm{m}/\mathrm{s}$)

(Take $\sqrt{2}=1.4$)

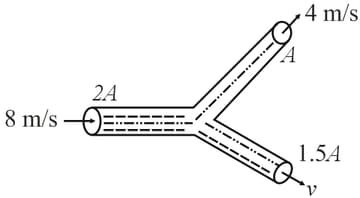
In the given figure, the velocity $v_3$ ( in $\mathrm{m} {\mathrm{s}}^{-1}$) will be

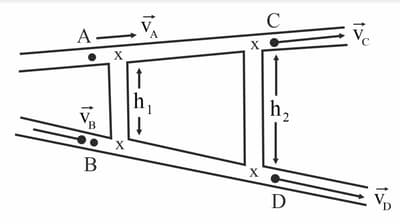
An ideal fluid is flowing in two pipes of the same cross-sectional pipe area. Both the pipes are connected with two vertical tubes, of length h₁ and h₂ as shown in the figure. The flow is streamline in both pipes. If the velocity of the fluid at A, B, and C are $2 \mathrm{m}/\mathrm{s}$, $4 \mathrm{m}/\mathrm{s}$, and $4 \mathrm{m}/\mathrm{s}$ respectively, the velocity of the fluid at $D$ (in m/s) is -

The cylindrical tube of a spray pump has a cross-section of 8.0 cm² one end of which has 40 fine holes each of diameter 1.0 mm. If the liquid flow inside the tube is 1.5 m/min, what is the speed of ejection of the liquid through the holes?

A horizontal pipe has a cross-section of $10$ ${\mathrm{cm}}^2$ in one region and of $5$ ${\mathrm{cm}}^2$ in another. The water velocity at the first is $5 \mathrm{m} {\mathrm{s}}^{-1}$ and the pressure in the second is $2\times {10}^5$. The pressure of water in $1^{st}$ region is given by $237.5\times {10}^{\mathrm{\alpha }} \mathrm{Pa}$. Then the value of $\alpha$ is.

If the velocity head of a stream of water is equal to $10 \mathrm{cm}$, then its speed of flow is approximately

A portion of a tube is shown in the figure. Fluid is flowing from cross-section area $A_1$ to $A_2$. The two cross-sections are at distance$।$ from each other. The velocity of the fluid at section $A_2$ is $\sqrt{\frac{g\ell }{2}}$. If the pressures at $A_1 \& A_2$ are same, then the angle made by the tube with the horizontal will be

Mumbai needs $1.4\times {10}^{12} \mathrm{L}$ of water annually. Its effective surface area is $600 {\mathrm{km}}^2$ and it receives an average rainfall of $2.4 \mathrm{m}$ annually. If $10\%$ of this rain water is conserved, it will meet approximately

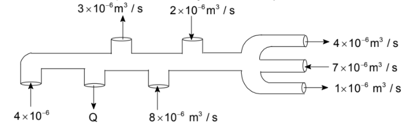
The pipe shows the volume flow rate of an ideal liquid at a certain time and its direction. What is the value of $Q$ in ${\mathrm{m}}^3/\mathrm{s}$ (Assume steady-state and equal area of cross-section at each opening)

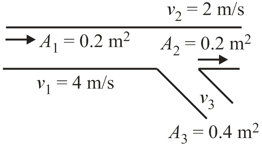
An incompressible liquid is flowing through a horizontal pipe as shown in figure. The value of speed $v$ is (areas are indicated in figure)

A vessel of area of cross-section A has liquid to a height H.There is a hole at the bottom of vessel having area of cross-section a. The time taken to decrease the level from ${\mathrm{H}}_1$ to${\mathrm{H}}_2$ will be (a <<A) :

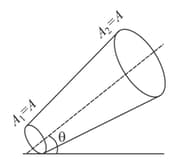
Calculate the ratio of speed, if the radii of the ends of a conical section of pipe are $0.1 \mathrm{m}$ and $0.04 \mathrm{m}$ is $\dots$

The total area of cross-section is $0.25 {\mathrm{m}}^2$. If the blood is flowing at the rate of $100 {\mathrm{cm}}^3/\sec$, then the average velocity of flow of blood through the capillaries is :