Velocity and Acceleration in Simple Harmonic Motion

Graph between velocity and displacement of a particle, executing S.H.M. is

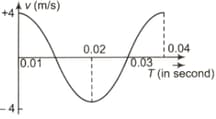
The velocity-time diagram of a harmonic oscillator is shown in the below figure. The frequency of oscillation is

The displacement-time graph of a particle executing SHM is as shown in the figure.

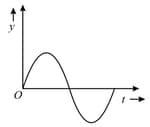
The corresponding force-time graph of the particle is

If the maximum velocity and acceleration of a particle executing SHM are equal in magnitude, the time period will be

Particle performing $\mathrm{S}.\mathrm{H}.\mathrm{M}.$ starts from extreme position. Plot a graph of displacement, velocity and acceleration against time.

Particle performing $\mathrm{S}.\mathrm{H}.\mathrm{M}.$ starts from mean position. Plot a graph of displacement, velocity and acceleration against time.

A body describes $\mathrm{S}.\mathrm{H}.\mathrm{M}.$ in a path $0.12\mathrm{m}$ long. Its velocity at the centre of the line is $0.12\mathrm{m}/\mathrm{s}.$ Find the period, and magnitude of velocity at a distance $\sqrt{3}\times {10}^{-2}\mathrm{m}$ from the central position.

A particle executes $\mathrm{S}.\mathrm{H}.\mathrm{M}.$ with amplitude of $10\mathrm{cm}$ and period of $10\mathrm{s}.$ Find the $\left(\mathrm{i}\right)$ velocity, $\left(\mathrm{ii}\right)$ acceleration of the particle at a distance $5\mathrm{cm}$ from the equilibrium position.

A particle is executing $\mathrm{S}.\mathrm{H}.\mathrm{M}.$ of amplitude $5\mathrm{cm}$ and period of  $2\mathrm{s}.$ Find the speed of the particle at a point where its acceleration is half of its maximum value.

The piston in the cylinder head of a locomotive has a stroke of $6\mathrm{ }\mathrm{m}$. If the piston is executing simple harmonic motion with an angular frequency of $200\mathrm{ }\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{ }\mathrm{m}{\mathrm{i}\mathrm{n}}^{-1},$ then maximum speed of the piston is

The velocity of a particle executing a simple harmonic motion is $13m{s}^{-1}$ , when its distance from the equilibrium position $\left(Q\right)$ is $3m$ and its velocity is $12m{s}^{-1}$ , when it is $5 m$ away from $Q$ . The frequency of the simple harmonic motion is

A particle performs SHM with an amplitude of $5 \mathrm{m}$. If at $x=4 \mathrm{m}$, the magnitude of velocity and acceleration are equal, then the time period of SHM (in seconds) is

A particle is moving such that its position is given by

$x=A\cos \omega t$

$y=A\sin \omega t$

$z=A\omega t$

Speed of particle will be

In case of a simple harmonic motion, if the velocity is plotted along the $\mathrm{X}-\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s}$ and the displacement (from the equilibrium position) is plotted along the $\mathrm{Y}-\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s}$ , the resultant curve happens to be an ellipse with the ratio: $\frac{\mathrm{m}\mathrm{a}\mathrm{j}\mathrm{o}\mathrm{r}\mathrm{ }\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s}\mathrm{ }\left(\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{ }X\right)}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{ }\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s}\mathrm{ }\left(\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{ }Y\right)}=20\pi$

What is the frequency of the simple harmonic motion?

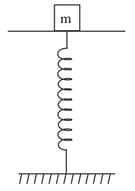
A mass of $2 \mathrm{kg}$ is put on a flat pan attached to a vertical spring fixed on the ground as shown in figure. The mass of the spring and the pan is negligible. When pressed slightly and released, the mass executes SHM. The spring constant is $200 \mathrm{N} {\mathrm{m}}^{-1}.$ What should be the minimum amplitude of motion, so that the mass gets detached from pan? $\left[\mathrm{G}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{n}, g=10 \mathrm{m} {\mathrm{s}}^{-2}\right]$

A particle of mass $m=5 \mathrm{g}$ is executing simple harmonic motion with an amplitude $0.3 \mathrm{m}$ and time period $\frac{\pi }{5}\sec$. The maximum value of force acting on the particle is

A particle is executing simple harmonic motion with an amplitude of 2m. The difference in the magnitudes of its maximum acceleration and maximum velocity is 4. The time period of its oscillation and its velocity when it is 1m away from the mean position are respectively.

A particle executing S.H.M. has a maximum speed of $30 \mathrm{cm} {\mathrm{s}}^{-1}$ and a maximum acceleration of $60 \mathrm{cm} {\mathrm{s}}^{-2}$. How much is the period (seconds) of the oscillation?

A large horizontal surface moves up and down in SHM with an amplitude of $1 \mathrm{cm}$. If a mass of $10 \mathrm{kg}$ (which is placed on the surface) is to remain continually in contact with it, the maximum frequency of S.H.M. will be

A particle is executing SHM along a straight line. Its velocities at distances ${\mathrm{x}}_1$ and ${\mathrm{x}}_2$ from the mean position are ${\mathrm{V}}_1$ and ${\mathrm{V}}_2$ respectively. Its time period is: