Spring-Mass System

A mass of $0.2\mathrm{kg}$ is attached to the lower end of massless spring of force-constant $200 \mathrm{N} {\mathrm{m}}^{-1}$, the upper end of which is fixed to a rigid support. Which of the following statement is/are true?

A block of mass $m$ is suspended by a rubber cord of natural length $l=m g / k$, where $k$ is force constant of the cord. The block is lifted upwards so that the cord becomes just tight and then block is released suddenly. Which of the following will not be true?

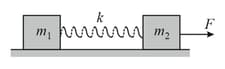
Two blocks connected by a spring rest on a smooth horizontal plane as shown in the given figure. A constant force $F$ starts acting on block $m_2$ as shown in the figure. Which of the following statements are not correct?

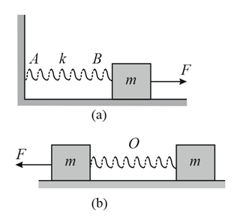
The given Fig. (a) shows a spring of force constant $k$ fixed at one end and carrying a mass $m$ at the other end placed on a horizontal frictionless surface. The spring is stretched by a force $F.$ Figure (b) shows the same spring with both ends free and a mass $m$ fixed at each free end. Each of the spring is stretched by the same force $F.$ The mass in case (a) and the masses in case (b) are then released. Which of the following statements are true?

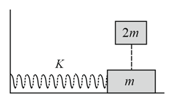
An object of mass $m$ is performing simple harmonic motion on a smooth horizontal surface as shown in the figure. Just as the oscillating object reaches its extreme position, another object of mass $2 \mathrm{m}$ is dropped on to oscillating object, which sticks to it. For this situation mark out the correct statement(s).

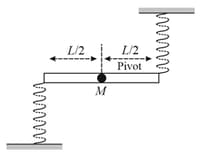
A uniform stick of mass $M$ and length $L$ is pivoted at its centre. Its ends are tied to two springs each of force constant $K.$ In the position shown in figure, the springs are in their natural length. When the string is displaced through a small angle $\theta$ and released, the stick

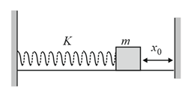
One end of a spring of force constant $K$ is fixed to a vertical wall and the other to a body of mass $m$ resting on a smooth horizontal surface. There is another wall at a distance $x_0$ from the body. The spring is then compressed by $3x_0$ and released. The time taken to strike the wall from the instant of release is (given ${\sin }^{-1}(1/3)=(\pi /9)$

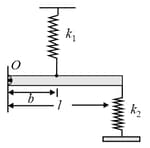
Two springs, each of unstretched length $20 \mathrm{cm}$ but having different spring constants $k_1=1000 {\mathrm{Nm}}^{-1}$ and $k_2=3000 {\mathrm{Nm}}^{-1},$ are attached to two opposite faces of a small block of mass $m=100 \mathrm{g}$ kept on a smooth horizontal surface as shown in the given figure.

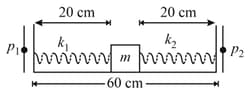
The outer ends of the two springs are now attached to two pins $P_1$ and $P_2$ whose locations are shown in the figure. As a result of this, the block acquires a new equilibrium position. The block has been displaced by small amount from its equilibrium position and released to perform simple harmonic motion; then

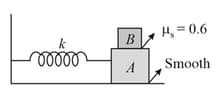
A block $A$ is connected to spring and performs simple harmonic motion with a time period of $2 \mathrm{s}.$ Another block $B$ rests on$A.$ The coefficient of static friction between $A$ and $B$ is ${\mu }_s=0.6.$ the maximum amplitude of oscillation which the system can have so that there is no relative motion between $A$ and $B$ is (take ${\pi }^2=g=10$)

Two springs with negligible masses and force constants $k_1=200 {\mathrm{Nm}}^{-1}$ and $k_2=160 {\mathrm{Nm}}^{-1}$ are attached to the block of mass $m=10 \mathrm{kg}$ as shown in the given figure. Initially the block is at rest, at the equilibrium position in which both springs are neither stretched nor compressed. At time $t=0,$ sharp impulse of $50 \mathrm{Ns}$ is given to the block with a hammer along the spring.

A body of mass $100 \mathrm{g}$ attached to a spring executes SHM of period $2 \mathrm{s}$ and amplitude $10 \mathrm{cm}.$ How long a time is required for it to move from a point $5 \mathrm{cm}$ below its equilibrium position to a point $5 \mathrm{cm}$ above it, when it makes simple harmonic vertical oscillations (take $g=10 \mathrm{m}/{\mathrm{s}}^2$) ?

A vertical spring carries a $5 \mathrm{kg}$ body and is hanging in equilibrium, an additional force is applied so that the spring is further stretched. When released from this position, it performs $50$ complete oscillations in $25 \mathrm{s},$ with an amplitude of $5 \mathrm{cm}.$ The additional force applied is

A block of mass $1 \mathrm{~kg}$ hangs without vibrating at the end of a spring whose force constant is $200 \mathrm{~N} / \mathrm{m}$ and which is attached to the ceiling of an elevator. The elevator is rising with an upward acceleration of $g / 3$ when the acceleration suddenly ceases. The angular frequency of the block after the acceleration ceases is

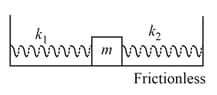
A spring of stiffness constant $k$ and natural length $l$ is cut into two parts of length $3l/4$ and $l/4,$ respectively, and an arrangement is made as shown in Figs. (a) and (b). If the mass is slightly displaced, find the time period of oscillation.

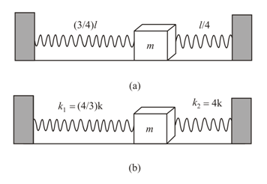
A small block is connected to one end of a massless spring of unstretched length $4.9 \mathrm{m}$. The other end of the spring is fixed as shown in the figure. The system lies on a horizontal frictionless surface. The block is stretched by $0.2 \mathrm{m}$  and released from rest at $\mathrm{t}=0$. lt then executes simple harmonic motion with angular frequency. $\mathrm{\omega }=\frac{\mathrm{\pi }}{3} \mathrm{rad}/\mathrm{s}$. Simultaneously at $\mathrm{t}=0$, a small pebble is projected with speed $\mathrm{v}$ from  point $\mathrm{P}$ at an angle of $45°$ as shown in the figure. Point P is at a horizontal distance of $10 \mathrm{m} \mathrm{from} \mathrm{O}$. If the pebble hits the block at $\mathrm{t}=1 \sec$, the value of $v$ is $:$
(take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$ )

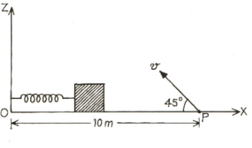
In the arrangement shown in the given figure, pulleys are small and light, and springs are ideal and $K_1=25{\pi }^2 \mathrm{N} {\mathrm{m}}^{-1}$, $K_2=2K_1$, $K_3=3K_1$ and $K_4=4K_1$ are the force constants of the springs. Calculate the period of small vertical oscillations of block of mass $m=3 \mathrm{kg}$.

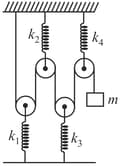
A rod of mass $m$ and length $l$ hinged at one end is connected by two springs of spring constants $k_1$ and $k_2$ so that it is horizontal at equilibrium. What is the angular frequency of the system? (in $\mathrm{rad} {\mathrm{s}}^{-1}$) (Take $l=1 \mathrm{m}, b=\frac{1}{4} \mathrm{m}, k_1=16 \mathrm{N} {\mathrm{m}}^{-1},$ $k_2=63 \mathrm{N} {\mathrm{m}}^{-1}$ and $m=3 \mathrm{kg}$)