Interference of Light Waves and Young's Experiment
Interference of Light Waves and Young's Experiment: Overview
This topic covers concepts such as Interference of Light Waves, Young's Double Slit Experiment, Terms in YDSE, Central Maximum and Numbering of Fringes, Importance of Slits and Holes in YDSE, Importance of Slit Width in YDSE, etc.
Important Questions on Interference of Light Waves and Young's Experiment
How the angular separation of interference fringes in Young’s double slit experiment would change when the distance between the slits and screen is doubled?
How the angular separation of interference fringes in Young’s double slit experiment would change when the distance between the slits and screen is doubled?
In Young’s double-slit experiment, monochromic light of wavelength illuminates the pair of slits and produces an interference pattern in which two consecutive bright fringes are separated by . Another source of monochromic light produces the interference pattern in which the two consecutive bright fringes are separated by . Find the wavelength of light from the second source.
In Young’s double slit experiment, monochromic light of wavelength 600 nm illuminates the pair of slits and produces an interference pattern in which two consecutive bright fringes are separated by 10 mm. Another source of monochromic light produces the interference pattern in which the two consecutive bright fringes are separated by 8 mm. Find the wavelength of light from the second source.
The effect on the interference fringes if the monochromatic source is replaced by a source of white light would be:
How the angular separation of interference fringes in Young’s double slit experiment would change when the distance between the slits and screen is halved:
In a Young’s double slit experiment, the two slits are kept apart and the screen is positioned away from the plane of the slits. The slits are illuminated with light of wavelength .
(i) Find the distance of the third bright fringe from the central maximum in the interference pattern obtained on the screen.
(ii) If the wavelength of the incident light were changed to , find out the shift in the position of third bright fringe from the central maximum.
A parallel beam of monochromatic light falls normally on a single narrow slit. How does the angular width of the principal maximum in the resulting diffraction pattern varies with the width of the slit?
How the fringe pattern changes when the screen is moved away from the slits:
In Young’s double slit experiment, the two slits 0.20 mm apart are illuminated by monochromatic light of wavelength 600 nm. The screen is 1.0 m away from the slits.
Find the distance of the second (i) bright fringe,
(ii) dark fringe from the central maximum.
In Young’s double-slit experiment, the two slits, apart, are illuminated by monochromatic light of wavelength . If the screen is away from the slits, then the distance of the second bright fringe from the central maximum is
Which of the following expressions is/are correct for Young’s experiment?
(i) condition for bright fringes
(ii) condition for dark fringes
ii) fringe width
In a Young’s double slit experiment, 12 fringes are observed to be formed in a certain segment of the screen when light of wavelength 600 nm is used. If the wavelength of light is changed to 400 nm, number of fringes observed in the same segment of the screen is given by
In a Young’s double slit experiment, fringes are observed to be formed in a certain segment of the screen when the light of wavelength is used. If the wavelength of light is changed to , number of fringes observed in the same segment of the screen is given by
In a double slit experiment, instead of taking slits of equal widths, one slit is made twice as wide as the other. Then, in the interference pattern
In Young’s double-slit experiment, the two slits act as coherent sources of equal amplitude 'A' and of wavelength . In another experiment with the same set-up the two slits are sources of equal amplitude 'A' and wavelength . but are incoherent. The ratio of the intensity of light at the midpoint of the screen in the first case to that in the second case is ______
In Young’s double-slit experiment, the two slits act as coherent sources of equal amplitude 'A' and of wavelength . In another experiment with the same set-up the two slits are sources of equal amplitude 'A' and wavelength . but are incoherent. The ratio of the intensity of light at the midpoint of the screen in the first case to that in the second case is ______
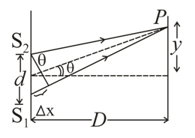
In an interference arrangement similar to Young’s double-slit experiment, slits are illuminated with coherent microwave sources each of frequency 1 MHz. The sources are synchronized to have zero phase difference. The slits are separated by distance d = 150.0 m. The intensity is measured as a function of where is defined as shown in figure. If is maximum intensity, calculate for
In Young's double-slit experiment, the distance between slits is and the distance of the screen from the slits. If the wavelength of light used is and is the intensity of central maximum, then the minimum distance of the point from the centre, where the intensity is is . What is the value of ?
In Young's double-slit experiment, the separation between the slits is and the distance of the screen from the slits is . When the wavelength of light used in the experiment is , the intensity at a distance from the central maximum is , where is the intensity of central maxima and and are the smallest integers. What is the value of ?
