Beats

Two sources of sound placed close to each other, are emitting progressive waves given by

${\mathrm{y}}_1 = 4\sin \left(600\mathrm{\pi t}\right)$ and ${\mathrm{y}}_2= 5\sin \left(608\mathrm{\pi t}\right)$.
An observer located near these two sources of sound will hear,

A tuning fork of frequency $512 \mathrm{Hz}$ is vibrated with a sonometer wire, and $6$ beats per second are heard. The beat frequency reduces if the tension in the string is slightly increased. The original frequency of vibration of the string is

A tuning fork vibrates with frequency $256 \mathrm{Hz}$ and gives one beat per second with the third normal mode of vibration of an open pipe. What is the length of the pipe? (speed of sound in air is $340 \mathrm{m} {\mathrm{s}}^{-1}$)

If two tuning forks $A \text{\& }B$ give $4 \mathrm{beats} {\sec }^{-1}$ with each other, on loading $A$ with wax, $2 \mathrm{beats} {\sec }^{-1}$ are given. If frequency of $A$ is $256 \mathrm{Hz}$, then frequency of $B$ is 

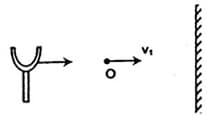
There is a source of sound (a tuning fork) moving towards a reflecting wall with a speed of $30 \mathrm{m} {\mathrm{s}}^{-1}$. The velocity of the sound in air is $330 \mathrm{m} {\mathrm{s}}^{-1}$ and the frequency of the tuning fork is $600 \mathrm{Hz}$. The observer is between the source and the wall and is moving with some velocity $V_1$ towards the wall. The beat frequency heard by the observer is $4 \mathrm{Hz}$. If the tuning fork is waxed, the frequency beats heard by the observer becomes $3 \mathrm{Hz}$. If the new frequency of tuning fork is $k$ then $\raisebox{1ex}{$k$}\!\left/ \!\raisebox{-1ex}{$50$}\right.$ is

Two tuning forks, $A$ and $B$ produce notes of frequencies $258 \mathrm{Hz}$ and $262 \mathrm{Hz}$. An unknown note sounded with $A$ produces certain beats. When the same note is sounded with $B$, the beat frequency gets doubled, The unknown frequency is

A closed organ pipe and an open organ pipe of same length produce $2 \mathrm{beats} {\mathrm{s}}^{-1}$ while vibrating in their fundamental modes. The length of the open organ pipe is halved and that of closed pipe is doubled. Then, the number of beats produced per second while vibrating in the fundamental mode is

Two tuning forks have frequencies $450 \mathrm{Hz}$ and $454 \mathrm{Hz}$ respectively. On sounding these forks together, the time interval between two successive maximum intensities will be _____.

Two waves each of loudness $L$ superimpose to produce beats. The maximum loudness of beats will be

Two whistles $A$ and $B$ have frequencies $660 \mathrm{Hz}$ and $590 \mathrm{Hz},$ respectively. An observer is standing in the middle of the line joining the two sources. Source $B$ and observer are moving towards the right with velocity $30 \mathrm{m} {\mathrm{s}}^{-1}$ and $A$ is standing to the left side. If the velocity of sound in air is $300 \mathrm{m} {\mathrm{s}}^{-1}$. The number of beats per second listened by the observer are,

A closed organ pipe and an open organ pipe of same length produce $2 \mathrm{beats} {\mathrm{s}}^{-1}$ while vibrating in their fundamental modes. The length of the open organ pipe is halved and that of closed pipe is doubled. Then, the number of beats produced per second while vibrating in the fundamental mode is

Two tuning forks, $A$ and $B$ produce notes of frequencies $258 \mathrm{Hz}$ and $262 \mathrm{Hz}$. An unknown note sounded with $A$ produces certain beats. When the same note is sounded with $B$, the beat frequency gets doubled, The unknown frequency is

An organ pipe, open from both ends produces $5$ beats per second when vibrated with a source of frequency $200 \mathrm{Hz}$ in its fundamental mode. The second harmonic of the same pipe produces $10$ beats per second with a source of frequency $420 \mathrm{Hz}$. The fundamental frequency of pipe is

Two closed pipes produce $10$ beats per second when emitting their fundamental nodes. If their lengths are in the ratio of $25: 26.$ Then, their fundamental frequency in $\mathrm{Hz}$, are

The frequency of tuning forks $A$ and $B$ are respectively $3\%$ more and $2\%$ less than the frequency of tuning fork $C$. When $A$ and $B$ are simultaneously excited $5$ beats per second are produced. Then the frequency of the tuning fork $A$ (in $\mathrm{Hz}$) is,

When two tuning forks $A$ and $B$ are sounded together, $x$ beat per second are heard. Frequency of $A$ is $n.$ Now, when one prong of fork $B$ is loaded with a little wax, the number of beats decreases. The frequency of fork $B$ is

A tuning fork of frequency $480 \mathrm{Hz}$ produces $10$ beats per second, when sounded with a vibrating sonometer string. What must be frequency of the string, if a slight increase in tension produces more beats per second than before?

An accurate and reliable audio oscillator is used to standardise a tuning fork. When the oscillator reading is $514,$ two beats are heard per second. When the oscillator reading is $510,$ the beat frequency is $6 \mathrm{Hz}$. The frequency of the tuning fork (in $\mathrm{Hz}$) is,

Two sound waves of length $1 \mathrm{m}$ and $1.01 \mathrm{m}$ in a gas produce $10$ beats in $3 \mathrm{s}$. The velocity of sound in gas is,

Two identical string instruments have frequency of $100 \mathrm{Hz}$. If tension in one of them increases by $4\%$ and they are sounded together, then the number of beats in $1$ second is,