Radioactivity

Two nuclei have mass numbers in the ratio $1:8$. The ratio of their nuclear radii would be:

The plot of the activity of a radioactive species versus time would be:

How long will a radioactive isotope, whose half life is $T$ years, take for its activity to reduce to ${\left(\frac{1}{8}\right)}^{\mathrm{th}}$ of its initial value?

Two nuclei have mass numbers in the ratio $8 : 125$. The ratio of their nuclear radii is:

The half life of a radioactive substance is$20$minutes. In how much time, the activity of substance drops to $\left(\frac{1}{16}\right)th$ of its initial value?

The half-life of a radioactive nucleus is $5$ years. The fraction of the original sample that would decay in $15$ years is :

Two radioactive elements $A$ and $B$ initially have same number of atoms. The half life of $A$ is same as the average life of $B$. If ${\lambda }_A$ and ${\lambda }_B$ are decay constants of $A$ and $B$ respectively, then choose the correct relation from the given options.

The decay constant for a radioactive nuclide is $1.5\times {10}^{-5} {\mathrm{s}}^{-1}$. Atomic weight of the substance is $60 \mathrm{g} {\mathrm{mole}}^{-1}$, $N_A=6\times {10}^{23}$. The activity of $1.0 \mu \mathrm{g}$ of the substance is ________ $\times {10}^{10} \mathrm{Bq}$.

The half life of a radioactive substance is $T$. The time taken, for disintegrating ${\left(\frac{7}{8}\right)}^{th}$ part of its original mass will be:

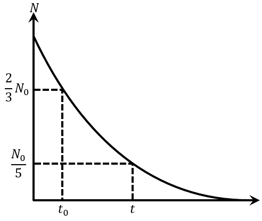
The graph shows the variation of the number of radioactive atoms left undecayed with time. The time $t$ corresponding to $N_0$ is:

Following statements related to radioactivity are given below :
(A) Radioactivity is a random and spontaneous process and is dependent on physical and chemical conditions.
(B) The number of undecayed nuclei in the radioactive sample decays exponentially with time.
(C) Slope of the graph of ${\log }_e$ (no. of undecayed nuclei) vs. time represents the reciprocal of mean life time $\left(\tau \right)$.
(D) Product of decay constant $\left(\lambda \right)$ and half-life time $\left(T_{\frac{1}{2}}\right)$ is not constant.

Choose the most appropriate answer from the options given below: 

A radioactive nucleus ${}_{\mathrm{Z}}{}^{\mathrm{A}}\mathrm{X}$ undergoes spontaneous decay in the sequence

${}_{\mathrm{Z}}{}^{\mathrm{A}}\mathrm{X}\to {}_{\mathrm{Z}-1}\mathrm{B}\to {}_{\mathrm{Z}-3}\mathrm{C}\to {}_{\mathrm{Z}-2}\mathrm{D}$, 

where $\mathrm{Z}$ is the atomic number of element $\mathrm{X}$. The possible decay particles in the sequence are:

Two radioactive samples $A$ and $B$ are initially in the ratio $1:4$, and have initial activities of the nuclei in the ratio $1:8$. If the half life of $A$ is $4$ years, choose the CORRECT statement(s)

A sample of ${\beta }^{-}$ active nuclei has a half life of $100 \min$. Initially, there are ${10}^{13}{\beta }^{-}$ active nuclei. Assume that all ${\beta }^{-}$ particles emitted leave the sample. What is the charge acquired (in $\mu \mathrm{C}$ ) by the sample in $200 \min$?

A large population of radioactive nucleus starts disintegrating at $t=0$. At time $t$, if $N=$ number of parent nuclei present, $D=$ the number of daughter nuclei present and $R=$ rate at which the daughter nuclei are produced, then the correct representation will be:

After $200$ days the activity of a radioactive sample reduces to $8000\mathrm{dps}$. After another $100$ days the activity reduces to $\frac{8000}{\sqrt{2}}\mathrm{dps}$. It can be said that

In ${\mathrm{U}}^{238}$ ore containing Uranium the ratio of ${\mathrm{U}}^{234}$ to ${\mathrm{Pb}}^{206}$ nuclei is $3$ . Assuming that all the lead present in the ore is final stable product of ${\mathrm{U}}^{238}$. Half life of ${\mathrm{U}}^{238}$ to be $4.5\times {10}^9$ years and find the age of ore is $A\times {10}^9$ years. Find $A$ rounded off to closest integer.

The ratio of the components in a mixture, which consists of two elements, is to be determined. The atomic number of the elements are big, their atomic mass numbers are the same and the amount of the sample is only $58 \mathrm{mg}$. We know that both elements undergo $\beta$ decay when they are bombarded by neutrons. They behave similarly when absorbing neutrons. The half-life of element $A$ is half an hour and the half-life of element $B$ is an hour. Right after the neutron irradiation the $\beta$ emission is measured. At this time $80$ particles are measured in $2$ seconds, and after an hour only $29$ particles are measured during $2$ seconds. Determine the mass of the element $A$ (in $\mathrm{mg}$) in the sample. Assume that spontaneous decay statistical law is obeyed by nuclei of both the elements.

Which of the following is a radioisotope?