Axiomatic Approach to Probability

Three identical dice are rolled. The probability that the same number will appear on each of them is

Determine  the chance that a non-leap year selected at random will not contain $53$ Sundays or $53$ Mondays?

Find the expectation of number of heads in $30$ tosses of a fair coin.

$A$ and $B$ throws a pair of dice. If $A$ throws $9$ and $B$'s chance of throwing a higher number is $\frac{k}{6}$, then the value of $k$ is _____

The Venn diagram illustrates the number of students taking each of the three sciences: physics, chemistry and biology.

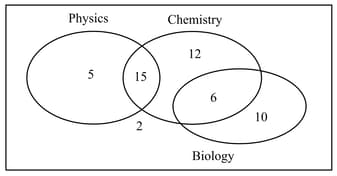
A student is randomly chosen from the group.

Find the probability that the student studies neither physics nor biology. (Write answer in simplest fraction form)

The Venn diagram illustrates the number of students taking each of the three sciences: physics, chemistry and biology.

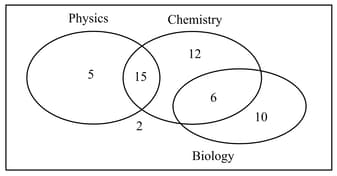
A student is randomly chosen from the group.

Find the probability that the student studies chemistry or biology. (Write answer in simplest fraction form)

In a survey, $48$ people were asked about their holidays over the past year. It was found that $32$ people had taken a holiday in Europe, and $25$ people had taken a holiday in the USA.

Everyone surveyed had been taken holiday to at least Europe or the USA. Find the probability that a randomly selected person had been taken holiday to Europe, but not the USA. (Write answer in simplest fraction form)

Xsquared Potato Crisps runs a promotion for a week. In $0.01\%$ of the hundreds of thousands of bags produced there are gold tickets for a round-the-world trip. Let $B$ represent the number of bags of crisps opened until a gold ticket is found.

Find $P\left(B=1\right), P\left(B=2\right)$ and $P\left(B=3\right)$.

Ten thousand $\mathrm{US}\$10$ lottery tickets are sold. One ticket wins a prize of $\mathrm{US}\$5000$, five tickets each win $\mathrm{US}\$1000$ , and ten tickets each win $\mathrm{US}\$200$. Find the probability of winning each prize in the lottery.

Chevy plays a game with four fair cubical dice numbered $\left\{1, 2, 3, 4, 5, 6\right\}$. She throws the four dice $160$ times and finds that the event "throw at least one $6$" occurs $77$ times. She wonders what the theoretical probability is. She finds the answer after critically considering these four representations of the problem. Identify the best representation and justify your answer. Identify the worst representation and justify your answer.

Tree diagram with each of the four throws represented as below, giving a total of $1296$ branches	A quick and easy calculation.	Tree diagram with each of the four throws represented as below, giving a total of $16$ branches	A quick and easy application of probability laws.
	$4\times \frac{1}{6}=\frac{2}{3}$		$1-{\left(\frac{5}{6}\right)}^4$

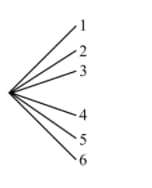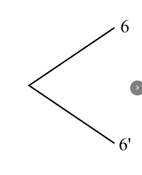A choir contains $15$ girls and $9$ boys.The choirmaster randomly selects four singers from the choir to be interviewed by a newspaper.Find the probability that at least one boy is in the four singers selected. 

Denise can catch a local bus or an express bus to take her to work each day. The probability she catches the local bus is $0.8$. If she catches the local bus, the probability that she is on time for work is $0.5$. If Denise catches the express bus, the probability that she is on time for work is $0.95$.

Hence calculate the probability that Denise will be late for work. (Round off and write up to $2$ decimal places)

Denise can catch a local bus or an express bus to take her to work each day. The probability she catches the local bus is $0.8$. If she catches the local bus, the probability that she is on time for work is $0.5$. If Denise catches the express bus, the probability that she is on time for work is $0.95$.

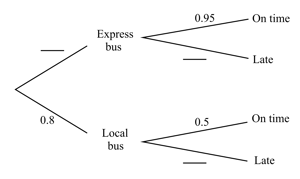
Copy and complete the tree diagram above.

Chevy plays a game in which she throws a pair of fair cubical dice numbered $\left\{1, 2, 3, 4, 5, 6\right\} 24$ times. Find the probability that she throws at least one double six.

A jewellery box contains $13$ gold earrings, $10$ silver earrings and $12$ titanium earrings. Two earrings are drawn with replacement. Find the probability that they are made of different metals.

(Round off and Write answer up to two decimal places)

The letters of the word $\mathrm{MATHEMATICS}$ are written on $11$ separate cards on shown below:

 A card is drawn at random then replaced. Then another card is drawn.

Let $A$ be the event the first card drawn is the letter $A$.

Let $M$ be the event the second card drawn is the letter $M$.  Find $P\left(A\right)$.

The discrete random variable $B$ has probability distribution function given by $\mathrm{P}\left(B=b\right)=k\left(4-b\right)$ for $b=0, 1, 2, 3$. Find $k$ and $\mathrm{E}\left(B\right)$.

Part of the discrete probability distribution of the discrete random variable $T$ with domain $\left\{1, 2, 3, 4, 5\right\}$ is shown in the bar chart.

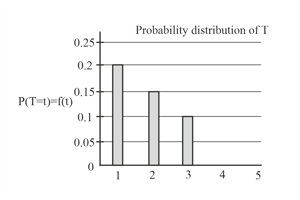
Given that $\mathrm{P}\left(T=4\right)=4\mathrm{P}\left(T=5\right)$, construct the probability distribution table for $T$.

Nico and Artem are designing a card game. In their pack of cards, each card has $2, 1, 0$ or $5$ printed on it. A card is selected from the pack and the number on the card defines a random variable $X$.

Artem correctly states that the probability distribution is:

Find the value of $p$.

(Write answer in decimal form)

Nico and Artem are designing a card game. In their pack of cards, each card has $2, 1, 0$ or $5$ printed on it. A card is selected from the pack and the number on the card defines a random variable $X$.

Nico states that the probability distribution of the game is as follows:

Explain why Nico is wrong.