Criteria for Congruence of Triangles

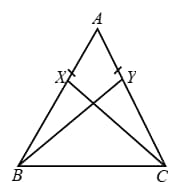
In Fig. X and Y are two points on equal sides $AB$ and $AC$ of a $∆ABC$ such that $AX = AY$. Prove that $XC = YB$.
  

$AD$ and $BC$ are equal perpendiculars to a line segment $AB$. Then $CD$ _____ $AB$. [bisects/trisects]

If $AD$ is an altitude of an isosceles triangle $ABC$ in which $AB = AC$. Then:

$ABC$ is an isosceles triangle in which altitudes $BE$ and $CF$ are drawn to equal sides $AC$ and $AB$ respectively. Then:

If $E$ and $F$ are the midpoints of equal sides $AB$ and $AC$ of a triangle $ABC$. Then:

What are the Rules of Congruency?

Line $l$ is the bisector of an angle $\mathrm{\angle }A$ and $B$ is any point on $l$. $BP$ and $BQ$ are perpendiculars from $B$ to the arms of $\mathrm{\angle }A$. Is $△APB\cong △AQB$ (Yes/No) ?

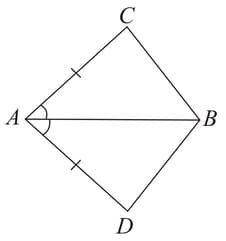
In quadrilateral $ACBD, AC=AD$ and $AB$ bisects $\angle A$ (see given figure). If $△ABC\cong △ABD.$ Is $BC=$$BD$ (Yes/No) ?

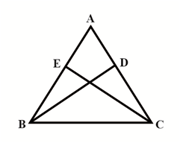
$ABC$ is an isosceles triangle with $AB=AC$. $BD$ and $CE$ are two medians of the triangle. Then $BD=$........

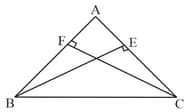
$\mathrm{A}\mathrm{B}\mathrm{C}$ is an isosceles triangle in which altitudes $\mathrm{B}\mathrm{E}$ and $\mathrm{C}\mathrm{F}$ are drawn to equal sides $\mathrm{A}\mathrm{C}$ and $\mathrm{A}\mathrm{B}$ respectively as shown in figure. The altitudes of the triangle are _____. (equal/unequal)

In Fig, $ABCD$ is a square and  $ABP$ is an equilateral triangle.Find the angles of $∆DPC.$(in degrees)

In a quadrilateral $ABCD$, $AB=CD$ and $\angle B=\angle C$. Prove that $AC=BD$.

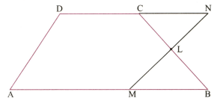
In a trapezium ABCD, $AB\parallel DC$ and L is the mid point of BC (Figure shown below). Through L, a line $MN\parallel AD$ is drawn to meet AB in M and DC produced in N. Prove that area $\left(ABCD\right)=$area $\left(AMND\right)$.

Which of the following is not a criterion for congruence of triangles?

The bisectors of the angles $B$ and $C$ of a $△$ $ABC$ meet at $P$. If $L, M$ and $N$ are the feet of the perpendiculars from $P$ to $BC, CA$ and $AB$ respectively, then prove that$PL=PM=PN$. 

Prove that the perpendiculars drawn from any point on the internal bisector of an angle, to the arms of the angle, are equal. 

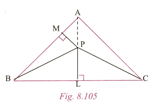
In Fig, $BP$ and $CP$ are bisectors of angles $B$ and $C$ respectively of $△ABC$ . If $PL\perp BC$   and  $PM \perp AB$, then prove that $△PMB\cong △PLB$

If the bisector of the vertical angle of a triangle bisects the base also, then the triangle is isosceles. 

Prove that, if the diagonals of a rectangle intersect each other at right angles, then it is a square.

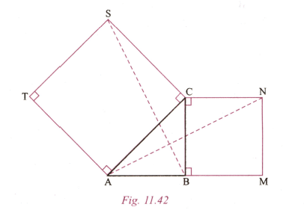
In Fig. 11.42, $∆ABC$ is a right-angled at $B$. $BMNC$ and $ACST$ are squares. Prove that $∆BCS$$\cong ∆NCA$. Prove that BS=AN