Vertical Circular Motion

Using energy conservation, derive the expression for the minimum speeds at different locations along a circular motion controlled by gravity. Is zero speed possible at the uppermost point? Also, prove that the difference between the extreme tensions (or normal force) depends only upon the weight of the object.

How do you find mass in circular motion?

What is the difference of tension between lowest and highest position of a point mass undergoing vertical circular motion under gravity?

What will happen to the string if tension at the uppermost point during vertical circular motion becomes zero?

How do you find mass in circular motion?

A pendulum string of length $𝓁$ moves up to a horizontal position as shown in figure and released.




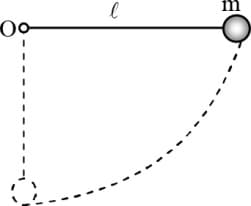
What should be the minimum strength of the string to withstand the tension as the pendulum passes through the position of equilibrium? The mass of the pendulum is $m$.

A biker initially at rest, starts to move on a circular path of radius $R=\frac{200}{7} \mathrm{km}$  with tangential acceleration $a = 1 \mathrm{m} {\sec }^{-2}$ (constant in magnitude). If on an average bike runs $50 \mathrm{km} {\mathrm{litre}}^{-1}$ and initially the bike has $2 \mathrm{litre}$ petrol. The minimum value of the coefficient of friction, so, that bike will not slip during motion is 

A circular curve of a highway is designed for traffic moving at $72 \mathrm{km} {\mathrm{h}}^{-1}$. If the radius of the curved path is $100 \mathrm{m}$, the correct angle of banking of the road should be given by

 In a Circus, a motor-cyclist having mass of $50 \mathrm{kg}$ moves in a spherical cage of radius $3 \mathrm{m}$. Least velocity with which he must pass the highest point without losing contact. 

A stone tied with a string, is rotated in a vertical circle. The minimum speed with which the string has to be rotated

A heavy mass is attached at one end of a thin wire and whirled in a vertical circle. The chances of breaking the wire are maximum when

A particle is tied to a string describes a vertical circular motion of radius $r$ continually. If it has a velocity $\sqrt{3gr}$ at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is

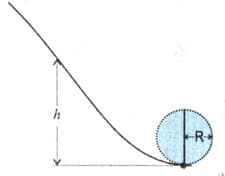
A ball is released from height along the slope and move along a circular track of radius $R$ without falling vertically downwards. Show that $h=\frac{5}{2}R$.

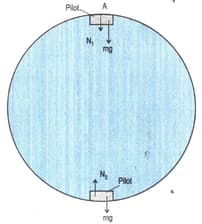
A pilot of mass $50 \mathrm{kg}$ in a jet aircraft executes a loop-the-loop with constant speed of $250 \mathrm{m}/\mathrm{s}$. If the radius of circle is $5 \mathrm{km}$, compute the force exerted by seat on the pilot at the bottom of loop.

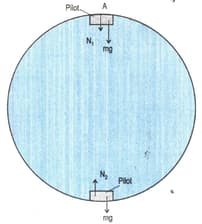
A pilot of mass $50 \mathrm{kg}$ in a jet aircraft executes a loop-the-loop with constant speed of $250 \mathrm{m}/\mathrm{s}$. If the radius of circle is $5 \mathrm{km}$, compute the force exerted by seat on the pilot at the top of loop.

An object of mass $0.5 \mathrm{kg}$ attached to a string of length $0.5 \mathrm{m}$ is whirled in a vertical circle at constant angular speed. If the maximum tension in the string is $5 \mathrm{kg}$ wt, calculate maximum number of revolutions it can complete in a minute.

An object of mass $0.5 \mathrm{kg}$ attached to a string of length $0.5 \mathrm{m}$ is whirled in a vertical circle at constant angular speed. If the maximum tension in the string is $5 \mathrm{kg} \mathrm{wt}$, calculate speed of object.

A stone weighing $1 \mathrm{kg}$ is whirled in a vertical circle attached at the end of a rope of length $0.5 \mathrm{m}$. Find the tension at highest position. 
 

A stone weighing $1 \mathrm{kg}$ is whirled in a vertical circle attached at the end of a rope of length $0.5 \mathrm{m}$. Find the tension at mid position. 
 

A stone weighing $1 \mathrm{kg}$ is whirled in a vertical circle attached at the end of a rope of length $0.5 \mathrm{m}$. Find the tension at lowest position.